In the previous part of the series we discussed how quantum theory prohibits copying of an arbitrary quantum state. In computing terms, this means that regardless of the richness of features provided by high-level quantum-specific languages such as Q#, we cannot implement a classical functionality of copy-and-paste on a quantum computer.

It turns out, however, that we can achieve a cut-and-paste type of effect, through a remarkable process of quantum teleportation.

Quantum teleportation 🔗

Quantum teleportation was theoretically proposed in a 1993 paper Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels by Charles Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres, and William Wootters.

The usage of the flashy name teleportation was justified by the authors in the following fashion:

We call the process we are about to describe teleportation, a term from science fiction meaning to make a person or object disappear while an exact replica appears somewhere else. It must be emphasized that our teleportation, unlike some science fiction versions, defies no physical laws. In particular, it cannot take place instantaneously or over a spacelike interval, because it requires, among other things, sending a classical message from Alice to Bob.

Few years after it was theoretically proposed, Anton Zeilinger and his team provided an experimental confirmation of the teleportation. In the summary of their experiment they reflected on the exciting new frontiers that lie ahead of quantum mechanics thanks to the realization of teleportation.

As any arbitrary state can be teleported, so can the fully undetermined state of a particle which is member of an entangled pair. Doing so, one transfers the entanglement between particles. This allows us not only to chain the transmission of quantum states over distances, where decoherence would have already destroyed the state completely, but it also enables us to perform a test of Bell’s theorem on particles which do not share any common past, a new step in the investigation of the features of quantum mechanics.

Mathematics of quantum teleportation 🔗

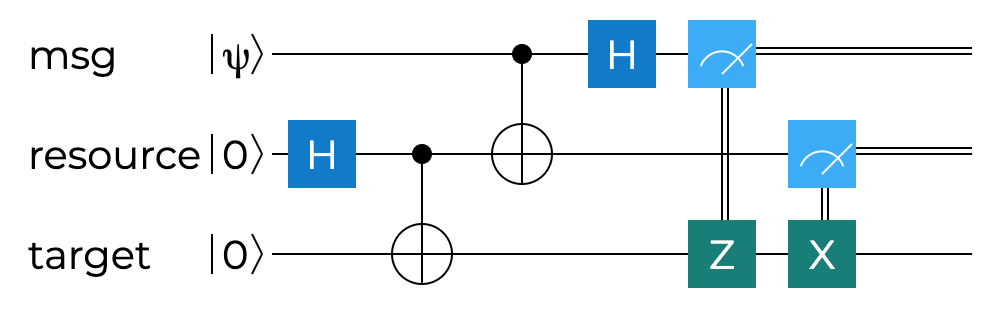
As we established earlier in this series, it is quite difficult, if not impossible, to develop a picture or intuition for quantum processes using our classical macroscopic thinking. Therefore - and this should be of no surprise, given that this is part 7 of this series already - the most reliable approach to attempt to reason about teleportation of quantum objects, even before we dive into Q# code, is to use the mathematical formalism of quantum mechanics, namely linear algebra. We already do know almost all the necessary constituent pieces - the CNOT gate, a number of single qubit gates or the phenomenon of entanglement in general. As we’ll see in a moment, we shall also require to perform the so-called Bell-basis measurement, but that is also something we briefly touched upon earlier.

The outgoing positions consist of Alice’s qubit in a superposition state $\ket{\psi_a}$, the one to be teleported, and an enatngled Bell state shared by Alice and Bob $\ket{\varphi_{ab}}$.

$$\ket{\varphi_{ab}} = \frac{1}{\sqrt{2}}(\ket{00} + \ket{11})$$

The first two kets in the equation describe Alice’s qubits, first the state to teleport, then her part of the entangled pair, while the last one describes Bob’s qubit, which is his part of the entangled pair and shall act as the target onto which the state $\ket{\psi_a}$ will be teleported. Next, Alice applies a $CNOT$ between the message $\ket{\psi_a}$ and her part of the entangled pair $\ket{\varphi_{ab}}$, with the qubit to be teleported as control

We can describe this mathematically in the following way:

$$\frac{1}{\sqrt{2}}(\alpha\ket{000} + \alpha\ket{011} + \beta\ket{110} + \beta\ket{101})$$

In the next step, Alice perform an $H$ on the message state leading to

$$\frac{1}{2}(\alpha(\ket{000} + \ket{011} + \ket{100} + \ket{111}) + \ \beta(\ket{010} + \ket{001} - \ket{110} - \ket{101})) = \ \frac{1}{2}(\ket{00}(\alpha\ket{0} + \beta\ket{1}) + \ket{01}(\alpha\ket{1} + \beta\ket{0}) + \ \ket{10}(\alpha\ket{0} - \beta\ket{1}) + \ket{11}(\alpha\ket{1} - \beta\ket{0}))$$

Finally, Alice measures both of the qubits in her possession. She could obviously obtain $\ket{00}$, $\ket{01}$, $\ket{10}$ or $\ket{11}$, and the significance of these results is that they are “influencing” the state of the entangled qubit in Bob is holding.

• when Alice measures $\ket{00}$, Bob’s qubit would end up in the state $\alpha\ket{0} + \beta\ket{1}$
• when Alice measures $\ket{01}$, Bob’s qubit would end up in the state $\alpha\ket{1} + \beta\ket{0}$
• when Alice measures $\ket{10}$, Bob’s qubit would end up in the state $\alpha\ket{0} - \beta\ket{1}$
• when Alice measures $\ket{11}$, Bob’s qubit would end up in the state $\alpha\ket{1} - \beta\ket{0}$

We can observe based in the above relations that:

• when Bob’s qubit ends up in the state $\alpha\ket{0} + \beta\ket{1}$, it is already the original state $\ket{\psi_a}$
• when Bob’s qubit ends up in the state $\alpha\ket{1} + \beta\ket{0}$, it is the equivalent to $X\ket{\psi_a}$
• when Bob’s qubit ends up in the state $\alpha\ket{0} - \beta\ket{1}$, it is the equivalent to $Z\ket{\psi_a}$
• when Bob’s qubit ends up in the state $\alpha\ket{1} - \beta\ket{0}$, it is the equivalent to $ZX\ket{\psi_a}$

This is where the classical information channel comes into play. For Bob to be able to restore the original state, he needs to be informed by Alice about her measurement outcomes. Therefore, she duly sends those results to Bob, and she can do it over any traditional communication channel. Based on that he simply needs to apply $X$, $Z$ or $ZX$ to his qubit, to be able to recover the exact message state.

Because the classical communication medium is required to exist between Alice and Bob to complete the protocol, even though the quantum state “moves” from location one to location two instantly, teleportation is not considered to violate special relativity because no information has been transferred - the classical channel holds the metadata needed for “decoding” the quantum state.

Qubit teleportation in Q# 🔗

Let us now write teleportation as a Q# program. It is of course a lot more exciting to consider teleportation with quantum communications networks over large distances, though the technological challenges related to it are still considerable. At the same time, even with a simple Q# program we will still be able to go through all the same steps that we outlined here, and we will succeed in orchestrating a real teleportation effect. Since we mentioned that the message to be teleported could be an arbitrary quantum state, we will do just that - and we will be teleporting a state specified in the Pauli X (Hadamard) basis ($\ket{+} ,\ket{-}$). We know that a superposition is base dependent so states $\ket{+}$ are $\ket{-}$ in a uniform superposition with respect to the Z-axis.

$$\ket{+} = H(\ket{0}) = \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$$
$$\ket{-} = H(\ket{1}) = \frac{1}{\sqrt{2}}(\ket{0}-\ket{1})$$

In order to make it more digestible, the code will be split into multiple blocks. The first part of Q# code looks as follows:

operation Teleport (signToSend : Bool) : Unit {
     using ((message, resource, target) = (Qubit(), Qubit(), Qubit())) {

        // prepare |-> or |+>
        if (signToSend == false) { X(message); }
        H(message);

        // create entanglement between resource and target
        H(resource);
        CNOT(resource, target);

        // reverse Bell circuit on message and resource
        CNOT(message, resource);
        H(message);

        // mesaure message and resource
        // to complete the Bell measurement
        let messageResult = MResetZ(message);
        let resourceResult = MResetZ(resource);

          // to do - decode the target based on
          // message and resource results
    }
}

We start off by preparing the $\ket{+}$ or $\ket{-}$ state based on the input parameter into the operation. As defined above, $\ket{+}$ is produced by applying an $H$ to $\ket{0}$, while $\ket{-}$ is created by applying $H$ to $\ket{1}$.

Once the message to teleport is prepared, we proceed to create a Bell state using the $resource$ and $target$ qubits. Next, a reverse Bell circuit is applied. This creates an entanglement between the $message$ and a $resource$. Finally, Alice measures both $message$ and $resource$ and shares her measurement outcome with Bob.

The snippet below shows Bob’s corrective actions depending on the results obtained by Alice.

// if we got |00>, there is nothing to do on the target
if (messageResult == Zero and resourceResult == Zero) { 
    Message("Measured |00>, applying I");
    I(target); 
} 

// if we got |01>, we need to apply X on the target
if (messageResult == Zero and resourceResult == One) { 
    Message("Measured |01>, applying X");
    X(target); 
} 

// if we got |10>, we need to apply Z on the target
if (messageResult == One and resourceResult == Zero) { 
    Message("Measured |10>, applying Z");
    Z(target); 
} 

// if we got |11>, we need to apply XZ on the target
if (messageResult == One and resourceResult == One) { 
    Message("Measured |11>, applying XZ");
    X(target); 
    Z(target); 
} 

let teleportedResult = Measure([PauliX], [target]);
Message("Teleported state was measured to be: " + (teleportedResult == Zero ? "|+>" | "|->"));
Reset(target);

We shall simply follow the rules we already defined - based on the results of Alice’s measurement, an $I$ , $X$, $Z$ or $XZ$ needs to be applied to the $target$ qubit. At the end, we can measure the qubit in the Pauli X basis. The obtained resulted will be either $\ket{+}$ or $\ket{-}$, which confirms to us that the original state was telported intact. If we measured it using the Pauli Z basis, we would obtain $\ket{0}$ or $\ket{1}$ with 50% probability each.

To cap things off, we can define the entry point operation for our Q# code and pass in the “sign” parameter we defined on the $Teleport$ operation - this would give us a chance to invoke the operation a number of times and compare the results.

@EntryPoint()
operation Start() : Unit {
        for (idx in 0..3) {
            Message("Teleporting |->");
            Teleport(false); // send |->
        }

        Message("***********");

        for (idx in 0..3) {
            Message("Teleporting |+>");
            Teleport(true); // send |+>
        }
}

The program repeats the teleportation of both $\ket{+}$ and $\ket{-}$ three times and produces something like this:

Teleporting |->
Measured |11>, applying XZ
Teleported state was measured to be: |->
Teleporting |->
Measured |11>, applying XZ
Teleported state was measured to be: |->
Teleporting |->
Measured |10>, applying Z
Teleported state was measured to be: |->
Teleporting |->
Measured |00>, applying I
Teleported state was measured to be: |->
***********
Teleporting |+>
Measured |00>, applying I
Teleported state was measured to be: |+>
Teleporting |+>
Measured |00>, applying I
Teleported state was measured to be: |+>
Teleporting |+>
Measured |11>, applying XZ
Teleported state was measured to be: |+>
Teleporting |+>
Measured |11>, applying XZ
Teleported state was measured to be: |+>

Final words 🔗

In the next part of this series, we shall continue exploring the interesting application scenarios around entanglement, by looking at a concept of “superdense coding”.