🎄 This post is part of the Q# Holiday Calendar 2022. 🎅🏻

In 1993, Avshalom Elitzur and Lev Vaidman from Tel-Aviv University wrote a paper in which they proposed a fascinating thought experiment. They described bombs equipped with a very sensitive triggering mechanism - through interaction with a single photon only - and then proceeded to show that using quantum effects, in a procedure they called “interaction-free measurement”, such bombs can be safely (without triggering the explosion) tested to determine whether a given bomb is armed or not.

We will explore this concept in this post using Q#, but since we do not want to have anything to do with the bombs, we will replace the original thought experiment with something much better - Santa’s gifts! 🎁

Introduction 🔗

Let’s imagine the following (completely plausible) scenario. Santa 🎅🏻 stores his gifts 🎁 in a warehouse, to which we can silently sneak it in order to peek into the gifts (and possibly re-arrange gift tags, right?). Now, Santa is very smart and knows that meddling kids tend to sneak up and peek around, so he installs quantum detectors in the gifts, which will trigger an alarm 🚨 on an interaction with even a photon - so really, as soon as someone tries to open the gift. Now, these detectors are expensive, so Santa only installs them in some of the gifts, but - in his opinion - this is already a good enough deterrent, since the kids will not be able to figure out which gifts are equipped with the alarms and which are not.

And as much as Santa is smart, with our knowledge of quantum effects, we should be able to outsmart him.

Interference 🔗

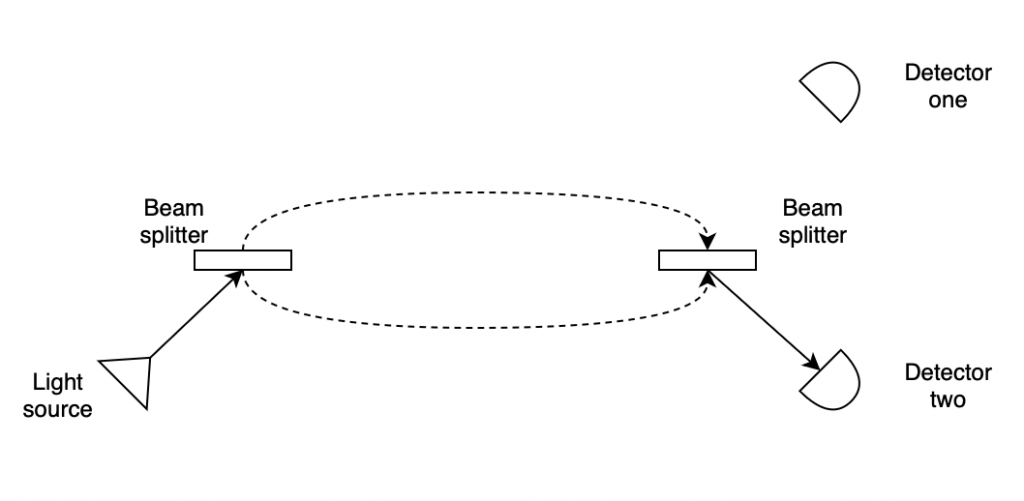
First let us consider a simplified description of Mach-Zehnder interferometer. The device (we leave out a number of optical details) is shown below, and consists of a light source (bottom left), two detectors (right side) and two beam splitters in the middle.

If we were to run this experiment in the lab, and if we were to send low frequency light (as close to single photons as we can get) through the interferometer, we will quickly notice something interesting. All the photons arrive at detector two only - why would that be? The answer to this lies in the interference phenomenon.

As the photon hits the first beam splitter, it has two possible paths it can go along - the upper one and the lower one - and quantum mechanics tells us that at this point it will enter the state of superposition of both of these possibilities. What does that actually mean depends on which interpretation of quantum mechanics you subscribe to; in the orthodox view the photon does not really exist until it is observed (which will only happen at the detectors), so in that sense the question is not even valid.

As soon as the photon reaches the second beam splitter, interference causes the photon to exit the superposition state and return to its original quantum state, which physically is now traveling only towards detector two. We can effectively say (after Paul Direac), that the photon interferes with itsel, though what this interference really means is not objectively agreed upon - it’s simply a consequence of the mathematical formalism of quantum mechanism. From a philosophical standpoint it depends, as earlier, on which interpretation makes most sense to you, or, more tangibly, whether you consider the wave function describing the photon to be ontic or epistemic.

We can model this loosely in Q# by using Hadamard transformation in place of the beam splitter:

// allocate a new qubit in default state |0⟩
use photon = Qubit();

// first beam splitter
H(photon);

// second beam splitter
H(photon);

// result is a certain Zero 
// which we can map to one of the detectors
let detectorResult = M(photon);

The important thing here is that this code produces a deterministic result, which matches well with the experiment from figure 1.

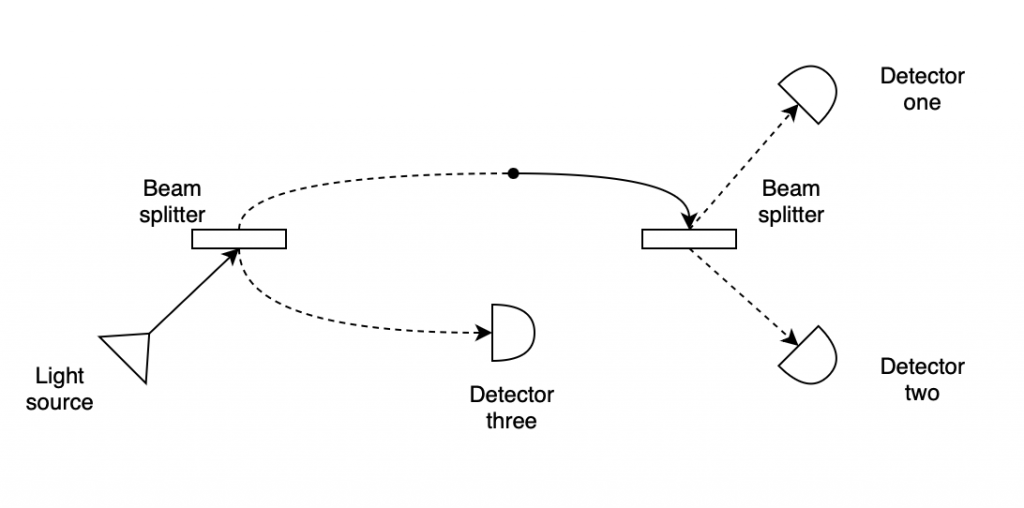
Even more interestingly, as soon as we try to detect the photon along one of the arms of the interferometer, the interference behavior disappears, as it’s outlined below.

In this setup, we place an additional detector on one of the paths inside the interferometer, to try to possibly absorb the photon earlier than before, and to find out which of the paths it is really traveling along when we say it’s in a “superposition”. As it turns out, this detector will record the presence of the photon in 50% of runs, randomly indicating to us that the photon is really present on the lower path in half of the experimental runs.

This also means that the photon reaches the second beam splitter only in 50% of cases, but since now we effectively “blocked” one of the two available paths, the photon is no longer in a superposition as it is known to travel on the upper path only, at which point it behaves differently - the two paths can no longer interfere with each other. As a consequence, the second beam splitter ends up doing the exact same thing as the first one did, namely forces the photon (back) into the superposition state. The photon then continues in this superposition until it is measured by the two terminating detectors, at which point it randomly shows up either at detector one or detector two. This is of course quite baffling.

We can reflect all of this in our simple Q# model by making small adjustments to the earlier code:

// allocate a new qubit in default state |0⟩
use photon = Qubit();

// first beam splitter
H(photon);

// detector three
let intermediateDetectorResult = M(photon);

// when One is measured
// assume the detector three absorbed the photon
if intermediateDetectorResult == Zero {
    // second beam splitter
    H(photon);

    // result is a certain Zero 
    // which we can map to one of the detectors
    let detectorResult = M(photon);
}

This code produces:

• intermediateDetectorResult = One in 50% of cases, which maps to detector three absorbing the photon
• intermediateDetectorResult = Zero and detectorResult = Zero in 25% of cases, which maps to photon showing up at detector one
• intermediateDetectorResult = Zero and detectorResult = One in 25% of cases, which maps to photon showing up at detector two

All of which corresponds to the experimental outcomes we described earlier.

Using interference against Santa 🔗

We can now apply this knowledge to trick dear old Santa. What would happen if we take Santa’s gift and place it (or, more specifically, it’s photon-sensitive alarm trigger) in the interferometer, instead of the intermediate detector three, as we saw in figure 2? Well, let’s model this in Q# and see.

We shall start by imagining the case were the gift does not have a working alarm. The Q# code is shown below, and it uses two qubits - q_tester as our photon and q_alarm to capture whether we have triggered Santa’s alarm.

use (q_tester, q_alarm) = (Qubit(), Qubit());

// corresponds to beam splitter one from earlier example
H(q_tester);

// since the alarm is not working, nothing happens
I(q_tester);

// corresponds to beam splitter two from earlier example
H(q_tester);

let detector = M(q_tester);
let alarmTriggered = M(q_alarm);

The code corresponds to our first interferometer example, with the notable addition of the I gate, which does nothing, since the gift has no working alarm (so no intermediate measurement happens).

Now, while two qubit measurements can reasonably produce four combinations of outcomes - $\ket{00}$, $\ket{01}$, $\ket{10}$ and $\ket{11}$ - it is easy to see that in this case the only possible outcome is $\ket{00}$ - since q_tester will experience interference and always produce a $\ket{0}$, while q_alarm starts and ends in state $\ket{0}$ too. In fact since the gift’s alarm is not working, the q_alarm never changes state at all and is not really needed in the program, but we include it to make this and upcoming code example symmetrical and easier to compare.

Let us now consider the alternative, namely a case where the alarm is really working. This is shown next:

use (q_tester, q_alarm) = (Qubit(), Qubit());

// corresponds to beam splitter one from earlier example
H(q_tester);

// there is now entanglement between the testing photon and the alarm being triggered
CNOT(q_tester, q_alarm);

// corresponds to beam splitter two from earlier example
H(q_tester);

let detector = M(q_tester);
let alarmTriggered = M(q_alarm);

The only difference is we replaced the I gate (which did nothing) with a CNOT between the two qubits. This means that we now have the following possible measurement outcomes (all equally likely, with 25% probability):

• $\ket{00}$, which means we don’t know whether q_tester exhibited interference or produced a random $\ket{0}$, and that alarm (q_alarm was $\ket{0}$) did not trigger. This outcome is indistinguishable from the outcomes of when the alarm was not working
• $\ket{01}$, which means we don’t know whether q_tester exhibited interference or produced a random $\ket{0}$, but it does not matter since we triggered the alarm (q_alarm was $\ket{1}$) and Santa caught us, and is now really angry
• $\ket{10}$, which means we know know for sure that q_tester exhibited no interference because it produced a random $\ket{0}$. Additionally, the alarm did not trigger (q_alarm was $\ket{0}$). This is a delightful outcome because it really tells us that the alarm is there and that it is working, but we managed to dodge it!
• $\ket{11}$, which means we know know for sure that q_tester exhibited no interference because it produced a random $\ket{0}$, which is great information for us, though it is useless since we triggered the alarm (q_alarm was $\ket{1}$) and Santa caught us, and is now really angry

We can reflect that in the Q# code in the following way, where the result is stored in a four item array, which would support running this code in multiple shots and keep count of accumulated totals:

mutable results = [0, size = 4];

// |00⟩ - inconclusive, Santa did not catch us
if (not detector and not alarmTriggered) {
    set results w/= 0 <- results[0]+1;
}

// |01⟩ - inconclusive, Santa alerted
if (not detector and alarmTriggered) {
    set results w/= 1 <- results[1]+1;
}

// |10⟩ - working alarm detected, Santa did not catch us
if (detector and not alarmTriggered) {
    set results w/= 2 <- results[2]+1;
}

// |11⟩ - working alarm detected, Santa alerted
if (detector and alarmTriggered) {
    set results w/= 3 <- results[3]+1;
}

In other words - when we get $\ket{00}$ we can retry further, $\ket{01}$ and $\ket{11}$ mean we were caught by Santa, while we are interested in outcome $\ket{10}$. This is already a massive step forward - as we have identified a way in which we can at least sometimes probe Santa’s gifts for alarms. The odds game is not high in our favor yet - 1 in 4 cases when the gift is really armed with an alarm, but it’s already better than what we started with, which is, well absolutely nothing.

Improving our probing strategy 🔗

Using similar principles, we can probe the gifts for alarms in an even better way, using the interaction-free measurement concept introduced by Elitzur and Vaidman.

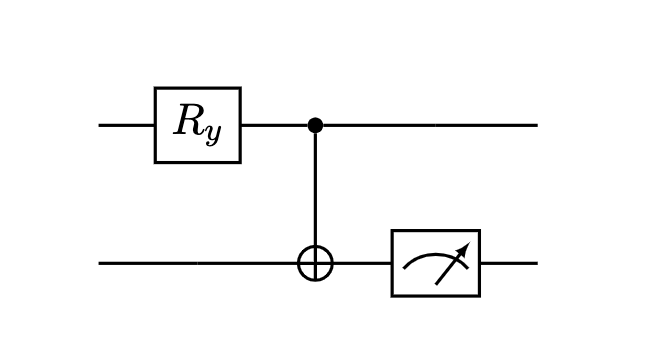
First, let’s consider the following circuit:

If we now apply $\mathbf{R_y^{\varphi}}$ to the first qubit, then the probability of reading out a $\ket{1}$ from that qubit upon its measurement is going to be $sin^2(\frac{\varphi}{2})$. Of course because we also go through a $\mathbf{CNOT}$, the two qubits are now entangled, so we can only end up with $\ket{00}$ or $\ket{11}$ for the overall system. This implies that if the second qubit measures to $\ket{1}$ (as we see on the circuit, we only measure the second one), the first one would also collapse to $\ket{1}$, and the alarm triggers. On the positive side, this only happens with the probability $sin(\frac{\varphi}{2})^2$, so the smaller the rotation angle, the less likely it is.

Overall the trick is to divide the $\pi$ into $n$ small rotation fractions to minimize the probability of triggering the alarm and then apply such tiny rotation to the first qubit, measure the second qubit and verify the alarm did not trigger. Next, we need to reset the second qubit back to $\ket{0}$, and rotate the first one by our tiny amount again and measure the second qubit again and so on. Any time we get a $\ket{1}$ from measuring the second qubit, means that triggered the alarm and alerted Santa, which will be the end of gifts for us, probably forever, as we are definitely going on a naughty list.

After $n$ repetitions, the rotations of the first qubit would add up so much that together they are equal to $\pi$, at which point we can stop and measure the first qubit too. The result of that measurement should also be $\ket{0}$ since the regular measurements of the second qubit would have “kept” the first qubit constantly at $\ket{0}$ too. Notice that if we instead did not have entanglement between the qubits, the rotations of the first qubit would have added up to flipping it to $\ket{1}$. In that case we would have discovered that the gift does not have a working alarm.

It is also easy to see that the higher the $n$, the better the chances of success. The probability of NOT triggering the alarm at each attempt is $cos(\frac{\varphi}{2})^2$, so using $n = 6$ rotational steps we already reach the probability of NOT triggering the alarm for all rotations equal to $cos(\frac{\pi}{12})^{12} \approx 66%$. And if we use many more small rotations, let’s say 100 of them, the probability of success already increases to $\approx 97.5%$.

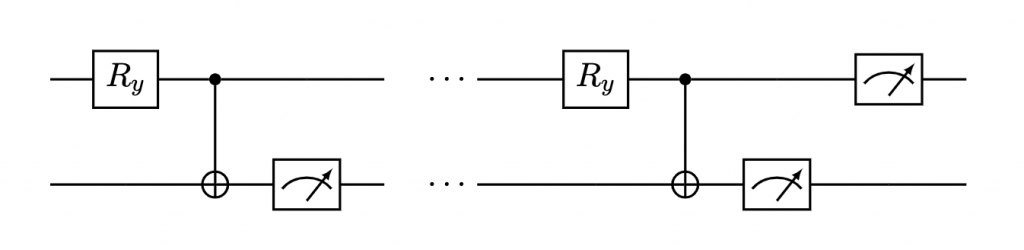
We can express all of that on the circuit by adding the extra iterations:

To summarize:

• if any of the intermediate $n$ measurements of the second qubit produced $\ket{1}$ the alarm was set off
• if the measurement of the first qubit (done at the end) produces $\ket{0}$, we have identified a working alarm without triggering it. We should stay away from this gift.

The same logic expressed in Q# is shown below, where $n$ is the amount of times we will slice $\pi$ to perform the rotations.

use (q_tester, q_alarm) = (Qubit(), Qubit());

mutable alarmTriggered = [Zero, size = n];
for j in 0..n-1 {
    // rotate by π/n
    Ry(PI()/IntAsDouble(n), q_tester);
    CNOT(q_tester, q_alarm);
    
    // we can now measure |00⟩ or |11⟩ only
    // the probability amplitude of triggering the alarm (second qubit measures to |1⟩) is now sin(π/n)
    set alarmTriggered w/= j <- M(q_alarm);
    Reset(q_alarm);
}

let workingAlarmIdentified = M(q_tester) == Zero;
let success = All(r -> r == Zero, alarmTriggered) and workingAlarmIdentified;

If we run this code with various values of n we will empirically find out that indeed as the n increases, so does our success probability.

Summary 🔗

In this rather absurd story we managed to use interaction-free measurements against Santa, and be able to determine which of his gifts we are able to peek into, and which are trapped with alarms. You can find the full source code for this post, including the orchestration for simulator that runs the examples a larger number of time, on Github. If you are further interesting in this topic Craig Gidney has an excellent blog post that goes even more in depth.

As we approach the holiday season, I wanted to also take a moment to wish all of you very happy and safe holidays. I hope that you are able to spend this special time of year with loved ones, and that the coming year brings you health, happiness, and success in all of your endeavours.