Last time we discussed the Quantum Fourier Transform - one of the important building blocks for more complex quantum algorithms. In this post, we will build upon that knowledge and take advantage of the QFT functionality, to explore another important subroutine that is used in many quantum programs, namely quantum phase estimation.

Background 🔗

The quantum phase estimation algorithm allows us, given an arbitrary unitary transformation $U$ which, when acting on its eigenvector $\ket{u}$, produces eigenvalue $e^{2{\pi}i\varphi}$, to estimate the phase $\varphi$.

$$
U\ket{u} = e^{2{\pi}i\varphi}\ket{u}
$$

In order to perform the estimation, we will need to allocate two separate qubit registers - one holding the eigenvector $\ket{u}$, and the other holding an arbitrary number of qubits. We will denote the amount of qubits in that register with $n$. The specific size of the register is corresponding to the level of precision that we’d like to have when performing the estimation, as well as to the probability of the success for the estimation itself. For better clarity, we shall call that register the “control register” - the reasons for that will become apparent in a moment. We will refer to the other register as the “eigenvector register” and use $t$ to describe its size. The eigenvector register sizeof $t$ is, naturally, depending on the amount of qubits needed to represent $\ket{u}$. Additionally, we also need to assume that we have access to a “black box” subroutine capable of performing a variant of $U$ transformation - namely, a controlled-$U^{2^j}$ for non-negative $j$ (${0,1,2..j}$).

The process begins by placing the control register in the uniform superposition by applying the $H$ gate to each of its $n$ qubits. However, we will take a two step approach here - the procedure is easier to reason about when initially considering a control register consisting of just a single qubit ($n = 1$), and therefore that’s what we will start with.

$$
\ket{\psi_1} = (H \otimes I^{\otimes t})(\ket{0}\otimes\ket{u}) = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})\ket{u}
$$

The next step is to apply controlled $U^{2^j}$ to both registers $n$ times - so depending on the size of the control register. At this point we should make one other observation. What happens when $U$ acts on its eigenvector $j$ times?

$$
UU…U\ket{u} = e^{2{\pi}i\varphi}e^{2{\pi}i\varphi}…e^{2{\pi}i\varphi}\ket{u} = e^{j2{\pi}i\varphi}\ket{u}
$$

The value of $j$ would be determined by:

$$j = n-1$$

In our initial simplified case we only have a single qubit in the control register, so we shall only apply controlled $U^{2^0}$.

$$
\ket{\psi_2} = CU^{2^0}\ket{\psi_1} = \frac{1}{\sqrt{2}}(\ket{0} + e^{2{\pi}2^0i\varphi}\ket{1})\ket{u}
$$

Since $2^0 = 1$, we can rewrite the state $\ket{\psi_2}$ into:

$$
\ket{\psi_2} = \frac{1}{\sqrt{2}}(\ket{0} + e^{2{\pi}i\varphi}\ket{1})\ket{u}
$$

This was the basic case for a control register with a single qubit. We are now in a position to provide a generalized version of the algorithm, by simply expanding the size of the control register. Below, we rerun the procedure where the control register contains any number $n$ qubits.

$$
\ket{\psi_1} = (H^{\otimes n} \otimes I^{\otimes t})(\ket{0}^{\otimes n}\otimes\ket{u}) = \frac{1}{\sqrt{2^n}}\sum_{j=0}^{2^n-1}\ket{j}\ket{u}
$$

Then we apply a sequence of controlled $U^{2^j}$ transformations.

$$
\ket{\psi_2} = \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{2{\pi}ki\varphi}\ket{k}\ket{u}
$$

We need to pause here to consider something very profound. As we learnt in the last post about Quantum Fourier Transform, QFT transformation produces the following result:

$$QFT\ket{k} = \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{\frac{2{\pi}ijk}{N}}\ket{k}
$$

If we substitute $N = 2^n$, this is very similar to the state we have reached in our $\ket{\psi_2}$ - if we omit the eigenvector register $\ket{u}$. In fact, we can extract the value of our $\ket{\varphi}$, by applying the adjoint (inverse) QFT! This is the critical point of the quantum phase estimation algorithm.

$$
\ket{\psi_3} = QFT^\dagger\ket{\psi_2} = \ket{\varphi}\ket{u}$$

In reality, as the name of the algorithm suggests, it will be an estimated value, however diving deeper into that is beyond the scope of this series. In an idealized example, what is left, is to measure the control register to obtain the approximated value of $\varphi$ which is of course what we have been after all along.

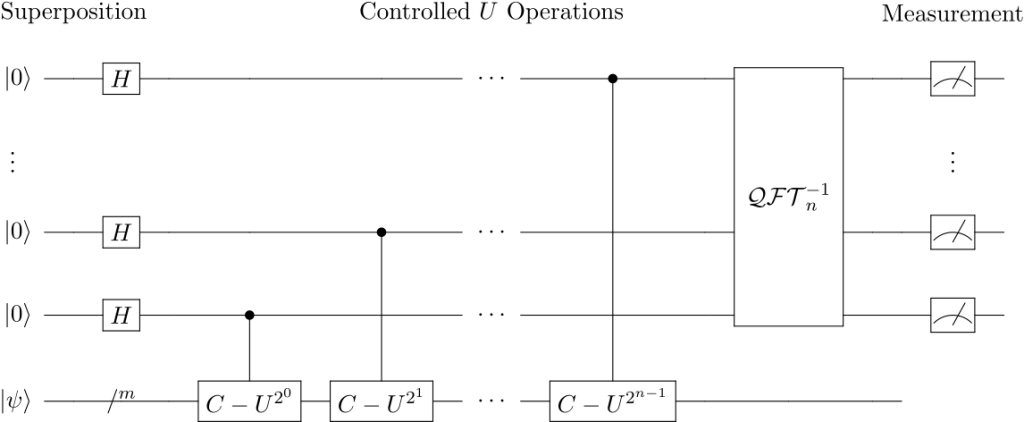
The overall circuit (after Wikimedia Commons) is shown below:

Q# implementation 🔗

With the theory under our belt, we will now shift our attention towards implementation of quantum phase estimation in Q#. Just like in the earlier examples, we will take two alternative approaches. The first one will be an implementation using low level gate primitives, which closely follows the circuit model, and the second one shall utilize the higher level features of Q# - highlighting its value for hassle-free development of generic quantum subroutines, as it ends eliminating some code that otherwise needs to be manually written.

Let’s start by defining our wrapper operation which can apply powers of $U$ to the given qubit state, and that supports the controlled functor as well.

An example of such a wrapper for $U$ equal to the $Z$ gate is shown below:

operation UZ(power : Int, qubits : Qubit[]) : Unit is Adj + Ctl {
    for _ in 1 .. power {
        Z(qubits[0]);
    }
}

Because the $Z$ gate acts on the single qubit, then the eigenstate is also single qubit - however we pass in an array, for reasons that will become apparent quite soon. In fact, the eigenstates of Z gate are $\ket{0}$ and $\ket{1}$ making this a rather trivial example - and a good one to start with.

We can create additional two simple operations that we can try our solution with - for gates $S$ and $T$:

operation UT(power : Int, qubits : Qubit[]) : Unit is Adj + Ctl {
    for _ in 1 .. power {
        T(qubits[0]);
    }
}

operation US(power : Int, qubits : Qubit[]) : Unit is Adj + Ctl {
    for _ in 1 .. power {
        S(qubits[0]);
    }
}

They share eigenvectors with the $Z$ gate, which will make our preparation simpler.

Equipped with these $U$ “blackboxes”, we can now define the operation that will perform the quantum phase estimation. The code is shown in the next snippet.

operation RunManualEstimation(eigenstate : Qubit, U : ((Int, Qubit[]) => Unit is Adj + Ctl), precision : Int) : Unit {
    use qubits = Qubit[precision];
    let register = LittleEndian(qubits);
        
    ApplyToEachA(H, qubits);

    for i in 0 .. precision - 1 {
        Controlled U([qubits[i]], (2^i, [eigenstate]));
    }

    Adjoint QFTLE(register);

    let phase = IntAsDouble(MeasureInteger(register)) * 360.0 / IntAsDouble(2^precision);
    Message($"Manual estimation result with precision {precision}: {phase} degrees");
    ResetAll(qubits);
    Reset(eigenstate);
}

As input to the operation we take the eigenstate, which we already know can fit in a single qubit, a delegate representing our $U$ “blackbox” and an integer defining the precision of our calculation.

We start by allocating the control register based on the precision value - this of course corresponds to the $n$ in our theoretical discussion earlier, and creating a uniform superposition over them. Next, we invoke the controlled-$U$ between each of the control register qubits and the eigenstate qubit, increasing the power of the gate with each subsequent qubit. Finally, we apply the adjoint (inverse) QFTLE - in this case we use the library functionality rather than doing that by hand because that is not really our focus here, so we don’t want to cloud the picture.

At that point everything that is left is to measure the control register to read out $\varphi$. In order to obtain a value in degrees, we have to do it in relation to 360 degrees and divided by the 2 raised to the power equal to our precision value. The reason of this is that the phase factor is a real number between 0 and $2\pi$ (in radians), and the propagation back into the control register depends on the precision level. For precision 1, we deal with $e^{i\varphi}$, then for precision 2 that’s $e^{2i\varphi}$, then $e^{4i\varphi}$ and so on. So the read out $\varphi$ has to be divided accordingly. To close things off, we also need, as always, to reset all of the involved qubits.

We can now test this simple Q# implementation by invoking our $RunManualEstimation$ operation against the 3 $U$ black-boxes prepared earlier. In each of the three cases, $Z$, $T$ and $S$, the eigenstate preparation will be the same - $I$ transformation for one, and $X$ transformation for the other. The code that does that for the $Z$ gate is shown below:

use eigenstate = Qubit();

Message("Z gate");
Message("Expected result: 0 degrees");
I(eigenstate);
RunManualEstimation(eigenstate, UZ, 3);
Message("Expected result: 180 degrees");
X(eigenstate);
RunManualEstimation(eigenstate, UZ, 3);

This prints out:

Z gate
Expected result: 0 degrees
Manual estimation result with precision 3: 0 degrees
Expected result: 180 degrees
Manual estimation result with precision 3: 180 degrees

The fact that the result is aligned with our expectation is very encouraging, so we should try it out for the other $U$ implementations as well. The code is almost identical.

Message("");
Message("T gate");
Message("Expected result: 0 degrees");
I(eigenstate);
RunManualEstimation(eigenstate, UT, 3);
Message("Expected result: 45 degrees");
X(eigenstate);
RunManualEstimation(eigenstate, UT, 3);

Message("");
Message("S gate");
Message("Expected result: 0 degrees");
I(eigenstate);
RunManualEstimation(eigenstate, US, 3);
Message("Expected result: 90 degrees");
X(eigenstate);
RunManualEstimation(eigenstate, US, 3);

And the output that we get at this point, should be:

T gate
Expected result: 0 degrees
Manual estimation result with precision 3: 0 degrees
Expected result: 45 degrees
Manual estimation result with precision 3: 45 degrees

S gate
Expected result: 0 degrees
Manual estimation result with precision 3: 0 degrees
Expected result: 90 degrees
Manual estimation result with precision 3: 90 degrees

The final part of this Q#-based implementation of the quantum phase estimation will have us turn our attention towards utilizing the built-in Q# functionalities instead of rolling out the procedure by hand as we just did. The existing $U$ black-boxes are still reusable in this case, but we will replace the operation $RunManualEstimation$ with $RunLibraryEstimation$. To make things easy to compare, we will keep the operation parameters identical.

Within the body of the operation, however, we will rely on the built-in $QuantumPhaseEstimation$ operation from the $Microsoft.Quantum.Characterization$ namespace. The complete code is shown below.

operation RunLibraryEstimation(eigenstate : Qubit, U : ((Int, Qubit[]) => Unit is Adj + Ctl), precision : Int) : Unit {
    use qubits = Qubit[precision];
    QuantumPhaseEstimation(DiscreteOracle(U), [eigenstate], BigEndian(qubits));

    let phase = IntAsDouble(MeasureInteger(LittleEndian(Reversed(qubits)))) * 360.0 / IntAsDouble(2^precision);
    Message($"Library estimation result with precision {precision}: {phase} degrees");
    ResetAll(qubits);
    Reset(eigenstate);
}

Just as before, we need to allocate a control register that corresponds in size to the precision level that was chosen. $QuantumPhaseEstimation$ operation takes as input a user-defined type $DiscreteOracle$, which wraps our $U$ definition. The signature of the $DiscreteOracle$ requires us to pass in a delegate that takes in a qubit array and an integer representing the power, which also, hopefully, makes it now clear why we took an array of qubits as input into the $U$ black boxes we created - we wanted to be able to use the $DiscreteOracle$ type. The other inputs into the $QuantumPhaseEstimation$ operation are a register containing the eigenstate (single qubit for us), and the control qubits wrapped with a $BigEndian$ QPU register. This is a little inconsistent, because most of the useful features of QDK are available in both big endian and little endian variants. Since we perform the measurement later using $MeasureInteger$ helper which requires $LittleEndian$ register, we need to reverse the qubits at that point. Other than that, the measurement procedure is the same as in our manual implementation.

We can now invoke the $RunLibraryEstimation$ and verify its results in a similar way as we did it earlier in the manual process. This is shown below for the sake of completness.

use eigenstate = Qubit();

Message("Z gate");
Message("Expected result: 0 degrees");
I(eigenstate);
RunLibraryEstimation(eigenstate, UZ, 3);
Message("Expected result: 180 degrees");
X(eigenstate);
RunLibraryEstimation(eigenstate, UZ, 3);

Message("");
Message("T gate");
Message("Expected result: 0 degrees");
I(eigenstate);
RunLibraryEstimation(eigenstate, UT, 3);
Message("Expected result: 45 degrees");
X(eigenstate);
RunLibraryEstimation(eigenstate, UT, 3);

Message("");
Message("S gate");
Message("Expected result: 0 degrees");
I(eigenstate);
RunLibraryEstimation(eigenstate, US, 3);
Message("Expected result: 90 degrees");
X(eigenstate);
RunLibraryEstimation(eigenstate, US, 3);

If we did everything correctly, we should see the following output:

Z gate
Expected result: 0 degrees
Library estimation result with precision 3: 0 degrees
Expected result: 180 degrees
Library estimation result with precision 3: 180 degrees

T gate
Expected result: 0 degrees
Library estimation result with precision 3: 0 degrees
Expected result: 45 degrees
Library estimation result with precision 3: 45 degrees

S gate
Expected result: 0 degrees
Library estimation result with precision 3: 0 degrees
Expected result: 90 degrees
Library estimation result with precision 3: 90 degrees

Summary 🔗

Quantum phase estimation, while on its own doesn’t seem particularly exciting, is one of the crucial building blocks for larger and more complicated quantum algorithms and solutions. In particular, it used as part of Shor’s factoring algorithm, arguably the crown jewel of all quantum algorithms invented up to this point, or in the quantum algorithm for linear systems of equations.

With quantum phase estimation covered, our journey in this particular introductory series is also nearing its end. In the next part of this series we will have a look at Shor’s algorithm.